2021. 11. 5. 16:14ㆍETC/ML & DL
Logistic Regression
로지스틱 논리 회귀의 이름은 회귀이지만 분류 모델로 볼 수 있습니다.
선형 회귀와 동일하게 선형 방정식을 학습하는데요.
종속 변수 (결과값)이 범주형일 때 사용합니다. 이 말은 아래 예시를 확인하고 나면 아주 잘 이해될 거에요.
로지스틱 회귀가 나온 이유에 대해 알아보면서 개념을 파악해보도록 할게요.
로지스틱 회귀는 논리 회귀라고 부르는데, 아래에서 제가 섞어 써도 이해해주세요!
만약, 시험 전 날 공부한 시간을 가지고 시험의 합격률을 예측하는 문제가 있다고 가정해봅시다.
이 문제에서 입력값은 '공부한 시간' 그리고 출력값은 '합격률'이 됩니다.
선형 회귀로 이 문제에 대한 그래프를 그려본다면 아래의 그림과 같습니다.

이상한 점을 느꼈나요?
만약, 입력값이 특정 범위를 벗어나게 되면 합격률이 음수가 되거나, 말도 안되게 커져버리는 거에요.
공부한 시간이 0시간이라면 합격률이 음수가 되어버리는 건 좀 너무하잖아요..
혹은, 20시간 이상이라면 합격 100%를 넘어버리는 허무맹랑한 데이터가 나옵니다.
만약 선형 회귀를 사용하면 이런 결과가 도출되고, 실생활에서는 이렇게 결과 데이터의 범위가 제한되는 경우가 많아요.
이런 경우를 종속 변수에 범주가 정해졌다고 말할 수 있겠죠.
이런 문제를 해결하기 위해 나온 것이 바로 로지스틱 회귀입니다.

로지스틱 회귀 그래프를 보니 느낌이 오시나요?
아무리 많은 시간을 공부해도 출력값은 최대치에 수렴하며, 아무리 공부를 하지 않아도 최소치에 수렴하게 돼요.
실제 많은 자연, 사회현상에서는 특정 변수에 대한 확률값이 선형이 아닌 S 커브 형태를 따르는 경우가 많다고 합니다.
이러한 S-커브를 함수로 표현해낸 것이 바로 로지스틱 함수 Logistic function입니다.
딥러닝에서는 시그모이드 함수 Sigmoid function라고 불립니다.
논리 회귀는 실질적인 계산은 선형 회귀와 똑같지만, 출력에 시그모이드 함수를 붙여 0에서 1사이의 값을 가지도록 합니다.
시그모이드 함수는 아래와 같이 생겼어요.
Sigmoid Function

$\sigma = \Large \frac{1}{1+e^{-x}}$
x가 음수 방향으로 갈 수록 y는 0에 가까워지고,
x가 양수 방향으로 갈 수록 y는 1에 가까워집니다.
즉, 시그모이드 함수를 통과하면 0 에서 1 사이 값이 나옵니다.
논리 회귀는 선형 회귀를 확장시켜 사용합니다.
아래의 그림과 같이 선형회귀를 사용할 때와 동일한 입력값을 주고, 동일한 결과값을 받죠.
그리고 결과값을 시그모이드 함수를 통해 범주를 제한하는 것입니다.

위의 그림을 선형회귀 때와 같이 수식으로 표현하면 아래와 같습니다.
$H(x) = \Large \frac{1}{1 + e^{-(Wx + b)}}$
Binary Cross Entropy
이진 로지스틱 회귀에서는 비용 함수로 MSE mean squared error를 사용하지 않고 BCE binary cross entropy를 사용합니다.
로그 손실을 최소화하기 위함인데요.
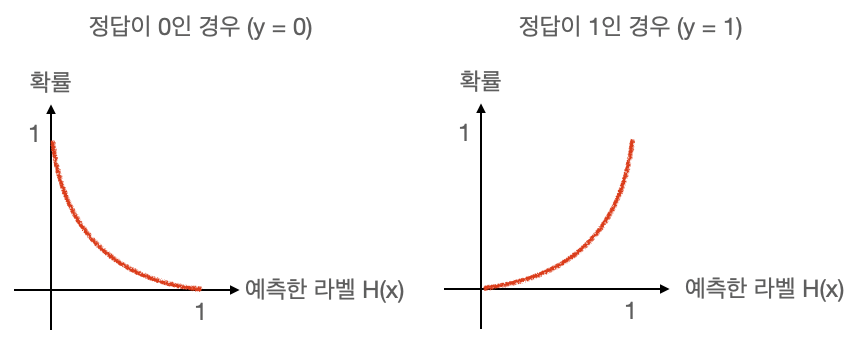
Binary Cross Entropy를 그래프로 개념을 이해하면,
임의의 입력값에 대해 우리가 원하는 확률 분포 그래프를 만들도록 학습시키는 손실 함수입니다.
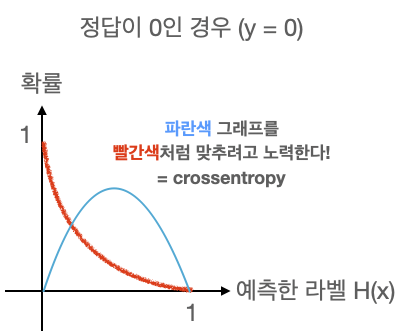
현재 학습 중인 입력값의 확률 분포가 파란색 그래프처럼 나왔다고 가정할 때, 정답이 0인 경우 빨간 그래프와 같이 만들어주기 위해 사용합니다. 그래서 keras의 crossentropy라는 함수는 파란색 그래프를 빨간색 그래프처럼 만들어주기 위해 노력하는 함수입니다. 선형 회귀를 했을때 정답값을 나타내는 점과 우리가 세운 가설 직선의 거리를 최소화하려고 했던 거리 함수와 비슷하게 생각하면 될 것 같아요.
Multinomial Logistic Regression
다항 로지스틱 회귀(multinomial logistic regression)란 종속변수 Y가 3개 이상의 범주를 가질 때 적용할 수 있는 로지스틱 회귀모델입니다. 단순히 확장된 개념이라 어렵지 않을 것 같아요.
예를 들면 대학교 시험 전 날 공부한 시간을 가지고 해당 과목의 성적(A, B, C, D, F)을 예측하는 문제처럼 여러개의 클래스 중 하나로 도출시키는 것입니다.
One-Hot Encoding
원핫 인코딩은 다항 분류 (Multi-label classification) 문제를 풀 때 출력값의 형태를 가장 예쁘게 표현할 수 있는 방법입니다.
다항 논리 회귀도 다항 분류에 속하기 때문에 원핫 인코딩 방법을 사용합니다.
여러개의 항을 0과 1로만 사용해서 표현하는데요. 위의 성적 예시를 가져와 원 핫 인코딩을 해보면 아래와 같이 만들어 집니다.
| 성적 | 클래스 | One-Hot Encoding |
| A | 0 | [1, 0, 0, 0, 0] |
| B | 1 | [0, 1, 0, 0, 0] |
| C | 2 | [0, 0, 1, 0, 0] |
| D | 3 | [0, 0, 0, 1, 0] |
| F | 4 | [0, 0, 0, 0, 1] |
원핫 인코딩을 만드는 방법은 아래와 같습니다.
- 클래스(라벨)의 개수만큼 배열을 0으로 채운다.
- 각 클래스의 인덱스 위치를 정한다.
- 각 클래스에 해당하는 인덱스에 1을 넣는다.
Softmax
Softmax는 선형 모델에서 나온 결과(Logit)를 모두가 더하면 1이 되도록 만들어주는 함수입니다.
다 더하면 1이 되도록 만드는 이유는 예측의 결과를 확률(=Confidence)로 표현하기 위함인데요.
우리가 One-hot encoding을 할때에도 라벨의 값을 전부 더하면 1(100%)이 되기 때문입니다.

그럼 여기까지 로지스틱(논리) 회귀에 대해 다뤄보았습니다 !
오류나 오타, 의견은 댓글로 적어주시면 감사하겠습니다 🙌🏻
참고
혼자 공부하는 머신러닝+딥러닝
[스파르타코딩클럽] 가장 쉽게 배우는 머신러닝
'ETC > ML & DL' 카테고리의 다른 글
| Deep Learning, Historical Review (0) | 2021.11.25 |
|---|---|
| Deep Neural Networks, 딥러닝 (0) | 2021.11.17 |
| Linear Regression (1) | 2021.11.04 |
| DeepSORT, 제대로 이해하기 (8) | 2021.10.08 |
| Pandas, 어렵지 않게 시작하기 2 - Dataframe (0) | 2021.09.15 |
Backend Software Engineer
𝐒𝐮𝐧 · 𝙂𝙮𝙚𝙤𝙣𝙜𝙨𝙪𝙣 𝙋𝙖𝙧𝙠