2021. 11. 4. 21:39ㆍETC/ML & DL
선형 회귀
가장 대표적인 회귀 알고리즘입니다.
선형 회귀 다양한 유형과 다양한 모델들이 나와있어요.
일반적으로 말하는 선형 회귀는 하나의 특성을 가지고 정답을 도출해나아가는 것을 의미해요.
가장 먼저, 회귀와 분류에 대한 구분을 하고 선형 회귀를 더 알아가보도록 할게요.
회귀 VS 분류
회귀 Regression : 임의의 어떤 숫자를 예측하는 문제
분류 Classification : 다수의 클래스 중 하나로 분류하는 문제
- 이진 분류 Binary classification
: 이진 클래스 Binary class 로 나눌 수 있는 문제. 출석을 했는지 안했는지를 구별할 때,
출석을 한 경우에는 1, 결석인 경우에는 0으로 측정하는 경우가 있습니다.
- 다중 분류 Multi class(or label) classification
: 여러 개의 클래스로 나누는 문제. 성적을 A, B, C, D, F 학점으로 나누는 경우가 있습니다.
회귀와 분류 둘 다 가능한 문제
예를 들어 사람 얼굴 사진을 분석 후 나이를 추측한다고 했을 때 회귀를 통해 나이를 추측할 수도 있지만,
10대, 20대, 30대, ... 로 여러 클래스의 형태로 나누어 추측할 수도 있습니다.
얻고자 하는 데이터에 따라 적절한 방식을 취하면 될 것 같네요.
Linear Regression
선형 회귀를 조금 더 사전적으로 말하자면 아래와 같아요.
선형회귀 Linear Regression
: 특성이 하나일 때, 그 특성을 가장 잘 나타낼 수 있는 직선을 학습하는 알고리즘
실제 데이터와 거리가 최소가 되는 아래의 직선의 방정식을 찾아내는 것이 이 알고리즘의 역할입니다.
$H(x) = Wx + b$
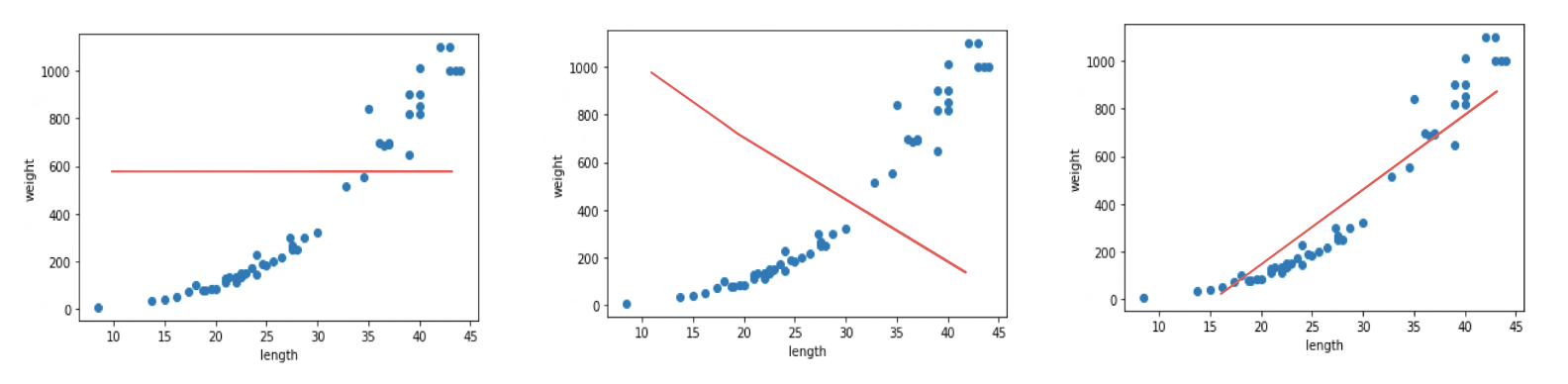
파란 점이 실제 데이터, 붉은 선이 예측한 직선이라고 할 때
실제 데이터를 가장 잘 나타내는 세 번째 그래프를 찾아내는 알고리즘입니다.
간단한 예시를 들어볼게요.
시험 전 날 마신 커피 잔 수에 따라 시험 점수를 예측하기
| 커피 잔 수 | 시험 점수 |
| 1 | 50 |
| 2 | 60 |
| 3 | 68 |
| 4 | 81 |
위의 데이터에서 커피 잔 수(특성 feature)에 따라 시험 점수(정답)를 예측하는 것을 선형 회귀로 풀어볼 수 있어요.
문제인 "시험 전 날 마신 커피 잔 수에 따라 시험 점수를 예측하기" 가 바로 가설이 되겠죠.
이걸 그래프로 그려보면 아래와 같습니다.
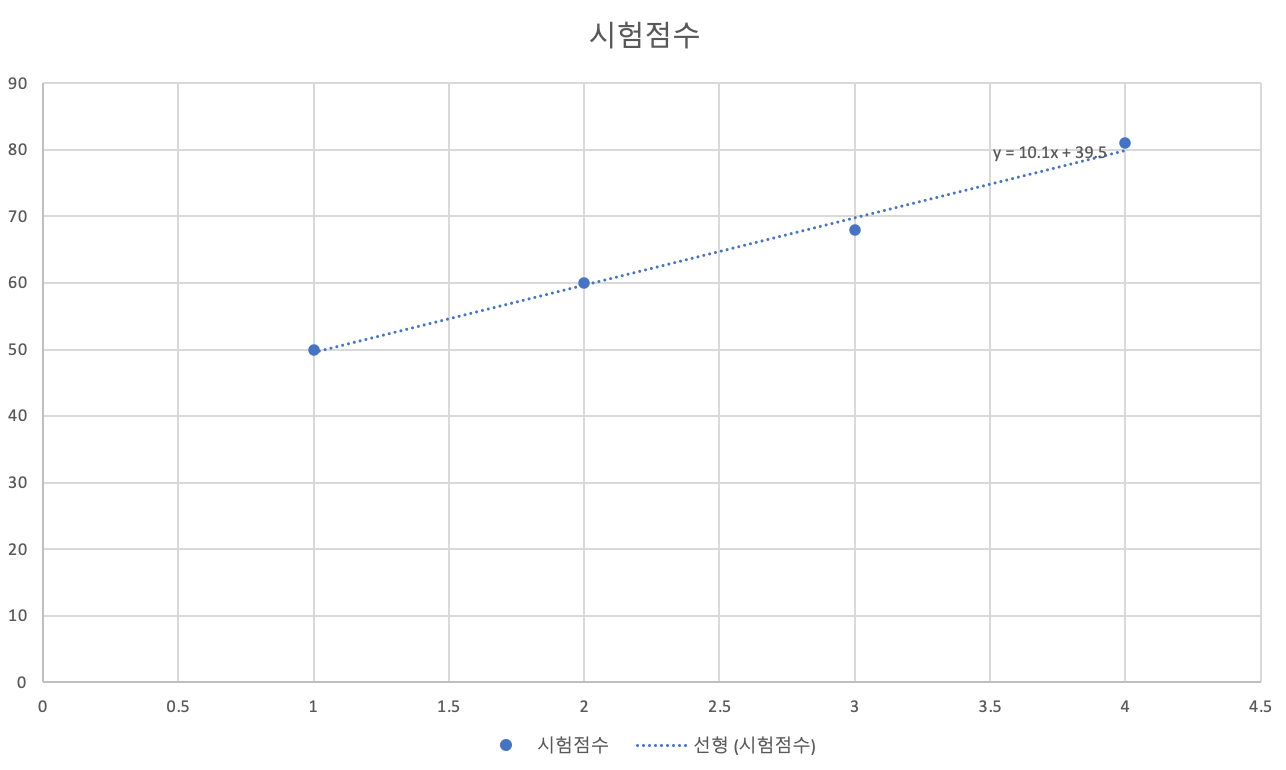
점이 정답이 되고, 점선이 바로 가설을 일차 함수로 표현한 것입니다.
아까 보았던 방정식 $H(x) = Wx + b$로 보면
가설 $H(x)$이 바로 점선이고, 점 $x$가 바로 feature가 됩니다.
Data Set
선형 회귀 코드를 살펴 보기 전에 데이터셋에 대해 알아볼게요.

선형 회귀로 훈련을 시킨 다음 얼마나 잘 훈련이 됐는지 테스트를 해봐야겠죠?
그래서 데이터들을 고루 나눠서 어떤 건 학습용 ~ 어떤 건 검증용, 또 테스트용으로 나눕니다.
많이 드는 예시가 시험이나 수능이에요. 학습하고 정답을 맞추는 것이 시험을 준비하는 것과 비슷해요.
우리가 시험을 본다고 할 때, 기출문제집 문제집을 가지고 공부를 하기 시작하죠.
이 때 기출문제집이 바로 학습용 데이터 Training Set입니다.
시험을 보기 전 모의고사를 통해 준비를 하죠. 이 때 모의고사는 검증 세트 Validation Set입니다.
그리고 시험이 바로 테스트 세트 Test Set입니다. 마지막으로 다시 정리를 해볼게요.
Training set
학습 데이터셋은 기출문제집이라고 했죠.
머신러닝 모델을 학습시키는 용도로 사용합니다. 전체 데이터셋의 약 80% 정도를 차지합니다.
Validation set
검증 데이터셋은 모의고사와 비슷하다고 했죠. 전체 데이터셋의 약 20% 정도를 차지합니다.
손실 함수, Optimizer 등을 바꾸면서 모델을 검증하는 용도로 사용합니다.
머신러닝 모델의 성능을 검증하고 튜닝하는 지표의 용도로 사용합니다.
이 데이터는 정답 라벨이 있고, 학습 단계에서 사용하기는 하지만, 모델에게 데이터를 직접 보여주지는 않으므로 모델의 성능에 영향을 미치지는 않습니다.
Test set
평가 데이터셋은 바로 시험입니다. 정답 라벨이 없는 실제 환경에서의 평가 데이터셋입니다.
검증 데이터셋으로 평가된 모델이 아무리 정확도가 높더라도 사용자가 사용하는 제품에서 제대로 동작하지 않는다면 소용이 없겠죠?
train_test_split
sklearn.model_selection.train_test_split(
*arrays, test_size=None, train_size=None, random_state=None, shuffle=True, stratify=None)
사이킷런에서는 데이터셋을 특정 비율로 나눠주는 함수를 제공합니다.
이름이 직관적이라서 이해하기 쉬울 것 같아요. 말 그대로 train set과 test set으로 분리해준다는 의미입니다.
하지만 여기서 test set보다는 validation set으로 사용합니다.
아래의 사용 예제를 보면 이해에 도움이 될 거에요.
Practice
선형회귀는 사이킷런으로 구해볼 수도 있고, Keras를 사용해서 구해볼 수도 있어요.
둘 다 간단하게 예시를 들어보도록 할게요.
1. Scikit-learn
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
train_input, valid_input, train_target, valid_target = train_test_split(
raw_input, raw_target, test_size=0.2, random_state=2021)
lr = LinearRegression()
lr.fit(train_input, train_target) # .fit() : train set으로 학습
lr.score(valid_input, valid_target) # .score() : validation set으로 평가 (결정계수를 평가)
lr.predict(test_input) # .predict() : test set으로 예측
위의 코드는 단순히 '이런 식으로 사용한다' 하는 코드에요.
위에 보면 결정 계수를 평가한다고 했는데요.
LinearRegression의 경우 score() 메소드는 분류일 땐 정확도를 평가하고,
회귀의 경우에는 결정계수(coefficient determination)을 계산합니다.
결정계수는 $R^2$는 대상을 얼마나 잘 설명할 수 있는가를 숫자로 나타낸 것입니다.
참고로 결정계수는 아래의 수식으로 계산됩니다.
$R^2 = 1 - \frac{\sum (Target-Prediction)^2}{\sum (Target-Mean)^2} = 1 - \frac{(타깃-예측)^2의 합}{(타깃-평균)^2의 합}$
어렵게 느껴질까봐 한글로 바꿔봤는데 효과가 좀 있나요..? ㅎㅎㅎㅎ
2. Keras
이번엔 딥러닝에서는 빠질 수 없는 keras를 이용한 방법을 사용해볼게요.
from sklearn.model_selection import train_test_split
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
from tensorflow.keras.optimizers import Adam, SGD
train_input, valid_input, train_target, valid_target = train_test_split(
raw_input, raw_target, test_size=0.2, random_state=2021)
model = Sequential([ Dense(1) ])
model.compile(loss='mean_squared_error', optimizer=Adam(lr=0.1)) #
model.fit(
train_input,
train_target,
validation_data=(valid_input, valid_target),
epochs=100)
# epoch ? 학습을 진행할 횟수 (option에서는 복수형인 것 체크하고 가기 ~)
# validation_data ? 검증 데이터를 넣어주면 한 epoch이 끝날때마다 자동으로 검증
test_pred = model.predict(test_input)
keras.Model.compile()
모델 설정한 후, 모델 학습 과정을 설정합니다. 모델을 학습하기 전 준비 단계입니다.
loss : 최적화 과정에서 최소화될 손실함수를 설정. mean_squared_error, binary_crossentropy를 주로 사용합니다.
optimizer : 훈련 과정을 설정하는 것으로, Adam, SGD 등이 있습니다.
keras.Model.fit()
모델을 학습합니다.
epochs : epoch라는 단어는 학습을 진행할 횟수를 의미합니다. 정확히는 단위입니다. 한 번 학습을 했을 때 1 에포크 라고 표현합니다.
validation_data : 검증 데이터를 넣어주면 한 epoch이 끝날때마다 자동으로 검증합니다.
keras.Model.predict()
학습한 모델을 통해 들어오는 데이터 값에 대한 예측을 반환합니다.
다중 선형 회귀
마지막으로 잠깐 다중 선형 회귀의 개념만 확인하고 마무리하겠습니다.
다중 선형 회귀는 Multi-variable linear regression 선형 회귀와 똑같지만 입력 변수가 여러개라고 생각하면 됩니다.
위에서 봤던 예시를 다시 가져오면,
커피 잔 수와 게임 플레이 시간 따른 당신의 시험 점수
| 커피 잔 수 | 게임 플레이 시간 | 시험 점수 |
| 1 | 3 | 45 |
| 2 | 4 | 52 |
| 3 | 5 | 33 |
| 4 | 2 | 81 |
위에서는 마신 커피 잔 수만 입력값으로 들어갔지만,
만약 입력값이 2개 이상이 되는 문제를 선형 회귀로 풀고 싶을 때 다중 선형 회귀를 사용합니다.
가설 $H(x_1, x_2, ..., x_n) = w_1x_1 + w_2x_2 + ... + w_nx_n + b$
손실 함수 $Cost = {{1\over N}\sum{(H(x_1, x_2, x_3, ..., x_n) - y) ^ 2}}$
오류나 오타, 의견은 댓글로 적어주시면 감사하겠습니다 🙌🏻
참고
혼자 공부하는 머신러닝+딥러닝
[스파르타코딩클럽] 가장 쉽게 배우는 머신러닝
'ETC > ML & DL' 카테고리의 다른 글
| Deep Neural Networks, 딥러닝 (0) | 2021.11.17 |
|---|---|
| Logistic Regression (0) | 2021.11.05 |
| DeepSORT, 제대로 이해하기 (8) | 2021.10.08 |
| Pandas, 어렵지 않게 시작하기 2 - Dataframe (0) | 2021.09.15 |
| Pandas, 어렵지 않게 시작하기 1 - Series (0) | 2021.09.08 |
Backend Software Engineer
𝐒𝐮𝐧 · 𝙂𝙮𝙚𝙤𝙣𝙜𝙨𝙪𝙣 𝙋𝙖𝙧𝙠